
- Annual Interest Rate (i), and
- Number of Years (n).
Discount Factors are available in data tables, such as the one shown in this pdf link, where we look up, for instance, the discount rate for 5% annual interest over 5 years is 0.7835. (Typically, these tables show different interest rates as columns and number of years in rows.) Alternatively, we can calculate the Present Value using the following equation.
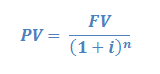
Let's look at a practical example. In five years we want to buy a house and we want to have a $100,000 down payment, so how much do we have to put away today? We can expect to earn 5% annual interest on our savings. Plugging these values into the equation above, we get the following.
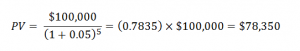
Of course, we can invert this equation and find out how much our investment today will be worth in the future. Let's say you will need a new car in three years and you are saving $100 every month. We will assume a 6% annual interest rate (i), or 0.5% per month (r). Instead of using the number of years (n), we will use the number of periods (N), or 36, for this example. So, we have a series of equations to solve where we look up the Future Value Factor in another table.
{C}{C}
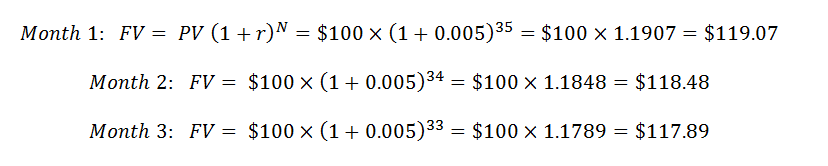
And so on, until we get to the final period.
{C}{C}
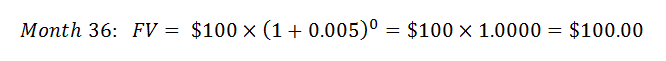
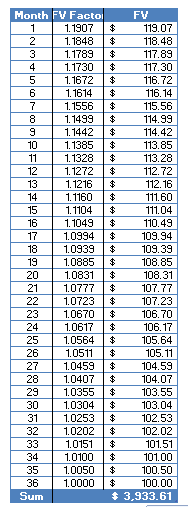
We then add up all the values of each month's savings to find out how much money we'll have saved in 3 years to buy a new car, which is $3,993.16. You can simplify the calculations by using an Excel spreadsheet, or better yet, using the Excel Formula FV (Future Value). When using Excel financial formulas, be careful to understand how it is setting the first period (e.g. whether it is "Month 0" or "Month 1").
This type of regular investment is called an "Ordinary Annuity (A)" and we can simplify the formulas to the following.
{C}{C}
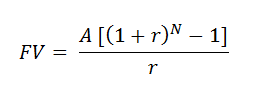
Just like the Discount Factor, we can also look up the Ordinary Annuity Factor in a table. Note that it is critical to consider the actual number of periods (months) and the periodic (monthly) interest rate. If we had assumed we were saving $1200 per year at 6% for 3 years, we find the Ordinary Annuity Factor is 3.1836 and we would then estimate savings of only $3,820.32, or a difference of about 4%. You can imagine if we were talking about millions of dollars for your project at the petrochemical plant that your boss would care about a difference of 4% if it amounts to more than $40,000! Your boss may also ask for the NPV, or Net Present Value, of your project. In this case, she wants to know if the net difference of all future cash inflows will exceed that of all future cash outflows. Most chemical engineering projects will require an initial capital investment, or cash outflow, in order to construct facilities. Only after the construction is completed will the product manufactured on that equipment be sold to realize cash inflows. Graphically, we can
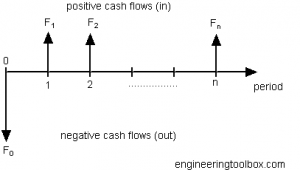
show the cash inflows and outflows on a Cash Flow Diagram. Let's assume that the process improvement will cost $20,000 immediately and then we will realize $5,000 profit per year annually for the next 5 years. We can calculate the Present Value (PV) of the $5,000 as an Ordinary Annuity (by combining and rearranging the above formulas for PV and for FV as a function of A). Then, we subtract the initial investment to find the NPV, where we assume a 5% annual interest rate.
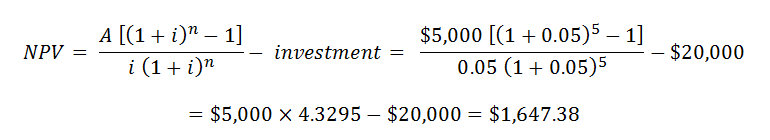
Note that if the initial investment had been $25,000, the project would present a losing proposition to the tune of over $3,000! Other ways that your boss may use Time Value of Money calculations is to perform "What If Studies". For example, "What if the alternative to investing $20,000 in the unit operations is to invest $20,000 in a bank deposit at 3% guaranteed interest?" We can then compare which alternative is more profitable for the company by using the calculations shown above. I hope that you have found this discussion on the Time Value of Money useful. You will use these calculations regularly both in your engineering life and in your personal life. And, though it's easy to plug numbers into an Excel formula (which I highly recommend), it is also vitally important that you understand the fundamental concepts behind the formulas. Next time, we'll look at how to read those ubiquitous Financial Statements that show up in your company's annual report.
What do Financial Statements really mean, anyway?
What's your experience with them?
By the way, the bank investment makes more money. Stay tuned for our next post on Financial Statements.



Comments
Teresa, this is a really informative post. You show how with a bit of thought and extra effort, people could really make a more compelling argument to their boss for taking on or not taking on project.
Great practical explanation.